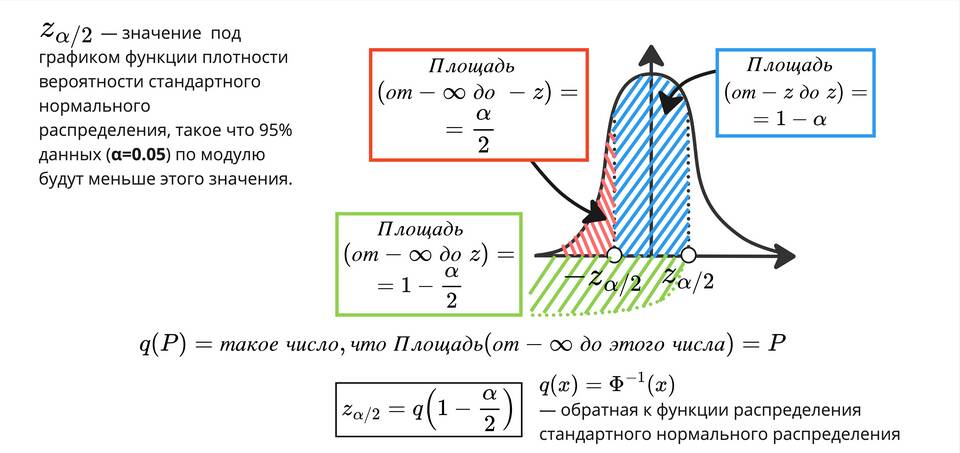
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение параметра генеральной совокупности. Рассмотрим методику его расчета.
Содержание
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение параметра генеральной совокупности. Рассмотрим методику его расчета.
1. Основные понятия
| Термин | Определение |
| Доверительная вероятность | Вероятность, с которой интервал содержит параметр (обычно 90%, 95% или 99%) |
| Стандартная ошибка | Мера изменчивости выборочного среднего |
| Критическое значение | Z-оценка или t-критерий для заданного уровня доверия |
2. Формула расчета доверительного интервала
2.1. Для среднего значения (известна σ)
ДИ = x̄ ± Z*(σ/√n)
- x̄ - выборочное среднее
- Z - критическое значение Z-распределения
- σ - стандартное отклонение генеральной совокупности
- n - объем выборки
2.2. Для среднего значения (неизвестна σ)
ДИ = x̄ ± t*(s/√n)
- Вычислите выборочное среднее (x̄)
- Определите стандартное отклонение выборки (s)
- Найдите t-критерий Стьюдента
- Рассчитайте стандартную ошибку
- Вычислите границы интервала
3. Пример расчета для 95% доверия
| Параметр | Значение |
| Выборочное среднее | 50 |
| Стандартное отклонение | 10 |
| Объем выборки | 30 |
| Доверительный интервал | 50 ± 3.58 |
4. Факторы, влияющие на ширину интервала
- Объем выборки (n) - обратная зависимость
- Доверительная вероятность - прямая зависимость
- Изменчивость данных - прямая зависимость
Практические рекомендации
Для малых выборок (n<30) используйте t-распределение Стьюдента. При известном стандартном отклонении генеральной совокупности применяйте Z-распределение. Проверяйте нормальность распределения данных перед расчетами.
